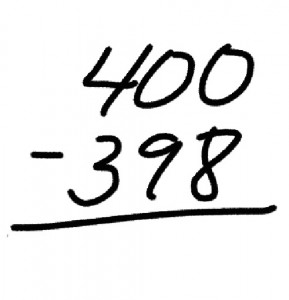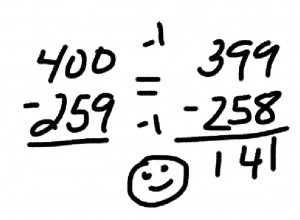Despite what has been said and written about me, I have no problem with the idea of students honing their math skills with repeated practice. Whether you are trying to master a jump shot or perfecting the tuning of your oboe, there is no substitute for practice. As the old lady told the dislocated young man when he inquired as to the best way to get to Carnegie Hall, “practice, young man, practice!”
However, I draw a deep line in the sand when it comes to those really basic “task cards” I see teachers using in their classrooms. The only positive thing I can say about them is that they’re only slightly less evil than those workbooks that they sell in aisle 5 of the local drug store.
Let’s be clear: just like there are “good” pirates (Jack Sparrow) and “bad” pirates (Somalis in polyester), the same is also true of practice. What does “bad” math practice look like? What frustrates me about many of the “task cards” I see is their almost obsessive focus on routine problems and therefore, very low levels of mathematical thinking. Do you really want your students to practice “regrouping across zeroes” using the problem shown below?
Truthfully, there are much better things you could do with 40 minutes of a school day than practicing this inane skill, but if you feel the need to satisfy whatever CCSS needs to be checked off that day, at least give problems that actually requires the skill to be used. If your students can’t calculate 400 – 398 without regrouping, then their problems with math are probably more serious than what can be accomplished with a task card.
If you feel the need to make a set of task cards that deals with “regrouping across zeroes,” then what you should not be doing is giving them a dozen identical problems that practices the skill over and over again. Believe me, they’ll forget how to do it within a few days anyway, and as Mark Twain said about teaching a pig to sing, it wastes your time and annoys the pig. Except that in this case, you’re wasting the students’ time AND annoying them. Since you probably just downloaded them from some silly website, it’s not like you have any skin in the game.
Okay, so you’ve read this so far and thinking, “okay, this guy is starting to make sense: if I’m going to have my students practice a skill, the least it should be conscientious and interesting. But I’m out of ideas: what should I do?” Here’s where my 30+ years of work in the field of mathematics education has some value: I’m going to give you 3, count them, 3 alternatives to doing the “standard” task card while still focusing on the skill in question (which is really not about regrouping across zeroes, but what you do when there are lots of zeroes in the minuend.)
Alternative Task Card Idea #1: Does it have to be so mindless? See that easy-peasy problem above? Why not put a whole bunch of them into the task card deck and ask students to sort the deck into problems that would require them to actually “regroup” from those that can be done through actual reasoning? Do we really want our student mindlessly regrouping problems that they can and should be solving in their heads?
Alternative Task Card Idea #2: Let’s make it a teaching tool. One of the things that makes me vomit bothers me about task cards is that they don’t help kids see alternatives to the tired and stale thinking that goes into memorizing and practicing an algorithm. If you’ve read my publication about how to teach subtraction “right” , then you’ll know about the importance of having your students understand that if you move both the minuend and subtrahend up or down the same amount, the difference will be the same. Using this principle, we can create a “twofer” task, which is that the student masters a somewhat important skill (solving a subtraction problem with lots of zeroes in the minuend) while reinforcing an essential concept that most teachers don’t know, understand or apply.
Alternative Task Card Idea #3: Let’s make it an assessment tool. There are different ways to test whether a student understands a concept, and reproducing an algorithm is probably the least comprehensive way to do this. I’ll call it “imitative assessment,” in all we are observing is whether the student can duplicate the exact same task shown to him/her by the teacher. Wouldn’t it be a better idea to assess a student so that we can determine higher levels of understanding? For example, what do you suppose we would learn from a student who completed this?
 I’m sure you can appreciate that there is a much higher level of thinking that needs to take place here, far beyond what is captured by mindlessly working out a procedure. The student here has to know something about place value, expanded notation, not to mention negative numbers. They also have to know how to perform rudimentary math calculations in their head (4,000 – 200, and 3,800 – 10.)
I’m sure you can appreciate that there is a much higher level of thinking that needs to take place here, far beyond what is captured by mindlessly working out a procedure. The student here has to know something about place value, expanded notation, not to mention negative numbers. They also have to know how to perform rudimentary math calculations in their head (4,000 – 200, and 3,800 – 10.)