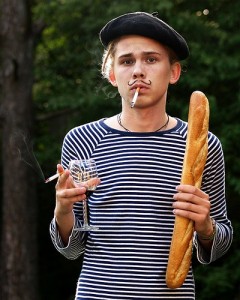Robert is an occasional reader of our hometown paper, The New York Times, and usually rolls his eyes whenever one of the cub reporters attempts to make sense of mathematics education. Every once in a while, however, the editors manage to slip up and allow someone with an ounce of common sense to write about his chosen field of expertise.
Such was the case when a reporter covered Andrew Hacker and his very convincing case for eliminating the traditional “advanced math” curriculum. We all know this as the algebra-geometry-trigonometry-advanced algebra, yadda, yadda, yadda forced march that college and capital accumulation bound high schoolers must march through. This sequence allegedly prepares the few students who actually understand this stuff for brilliant careers in art history, restaurant management and human resource development. It’s not that Hacker dislikes mathematics or wants to dumb it down; rather, he suggests that maybe a more thoughtful approach focusing on “real life” uses of mathematics would actually achieve the goals we have set out: prepare our students to participate in our quasi-capitalistic economic life and pseudo-democratic political system.
While we’re at it, Robert wishes Hacker would also take a more courageous stand, and push back against the teaching of fractions in the elementary grades. Talk about a waste of time: while fractions were a useful thing to know if you were a working class Sumerian over 5 millennia ago, today they’re just that like that unwelcome uncle who pops up at the Thanksgiving dinner table each year: nobody knows why he’s there, and everybody would digest much easier if he just stayed in his cardboard box.
 As Robert tells it, fractions had a good run, and with a 5,000+ year history, they’ve outlived every fad imaginable, including paisley togas and virgin sacrifices. Fractions began their long run with the Egyptians, who utilized them to divide up plots of land and levy taxes. The ancient Sumerians loved fractions so much that they invented the 24 hour day, the 60 minute hour and the 360 degree circle just so they could divide them up into equal pieces really easily: a 24 hour day can be divided into halves, thirds, quarters, sixths, 8ths, 12ths and 24ths (don’t get me started on how easy it is to divide 60 and 360….) You just can’t do that with 10 or 100.
As Robert tells it, fractions had a good run, and with a 5,000+ year history, they’ve outlived every fad imaginable, including paisley togas and virgin sacrifices. Fractions began their long run with the Egyptians, who utilized them to divide up plots of land and levy taxes. The ancient Sumerians loved fractions so much that they invented the 24 hour day, the 60 minute hour and the 360 degree circle just so they could divide them up into equal pieces really easily: a 24 hour day can be divided into halves, thirds, quarters, sixths, 8ths, 12ths and 24ths (don’t get me started on how easy it is to divide 60 and 360….) You just can’t do that with 10 or 100.
But Robert maintains, fractions are pretty much dead so far as common usage goes, and you can blame that on the French. Yes, those Jerry Lewis and croissant beurre loving eggheads are to blame for the downfall of fractions and the rise of its bitter opponent, the easy and convenient (and mostly sanitary) decimal notation. Quelle barbe!
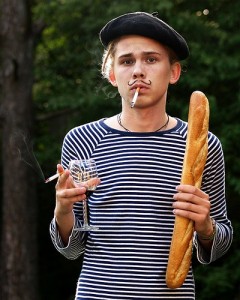
Typical French citizen holding 300 ml glass of wine with 1 meter long baguette and smoking 100 mm cigarette. He’ll probably live to be 100 years old….
Whatever your feelings for the French, which can be determined by what you call fried potatoes served with ketchup, you’ll have to admit they were on to something by inventing and then adopting the metric system: it’s soooo easy to use! No one who has ever worked with kilograms, meters or liters (as well as newtons, joules and candela) has ever had to struggle finding a common denominator, convert to a mixed number or inverting and multiplying. Is it any wonder that 99.9% of all the countries in the world use decimal units of measurement?
But here in the United States, we love our fractions, which means that it is the only place on earth (well, toss in Liberia and Myanmar) where fractions have to be taken seriously. Open a cookbook and what do you find? Fractions of a pound, fractions of a cup, fractions, fractions, fractions! Robert believes cooking is a pretty pleasurable experience, up there with consensual sex, open-water swimming and playing the concertina, but when you mix in fractions, well, you’re just asking for trouble. Robert wagers that there is a significant fraction of the American population which hates to cook because they’re scared of fumbling with quarter cups and half-pounds.

Sorry, daughter, no cupcakes for your birthday: daddy doesn’t like baking with fractions…
Open a cookbook anywhere else in the world, and there will be nary a fraction in sight: everything will be measured in grams, kilograms and liters, which makes life quite a bit easier. Don’t need an entire kilogram? Just put a decimal point on it, baby! Need to increase a recipe by ten times? Push those digits one place to the left and move on! You just can’t do any of that with half-tablespoons of vanilla…..
And this just has to do with cooking; the prevalence of fractions in American life, from our use of 8 1/2 x 11″ sheets of paper for correspondences to road signs which tell us our exit is 3/4 of a mile away is just so passé. I agree: I know decimals will take some getting used to when it comes to our everyday life, but can’t we give it chance?

My best seller!
Truthfully, Robert loves teaching fractions, and even makes a pretty good living off of them, seeing as how 4 of the top 5 bestsellers at his online store are about… fractions! Even I think they have some important uses, especially when it comes to algebraic notation, and they can be rather fun when done in a playful and non-threatening way.

I really don’t think this is going to fix the problem…
However, in an era of high-stakes testing and curriculum standardization, maybe it’s time we reconsider the teaching of fractions in elementary school. Fractions prevent our students from solidifying more important concepts and mastering developing skills. They are confusing and have limited uses, yet we persist in teaching them to children who are just not equipped to understand them. Can we agree to delay them until 5th, 6th or 7th grade, when kids are more able to comprehend them, and can be covered in 1/4 the time?
I would wager that 93/95 of the American population would agree with me.
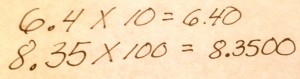
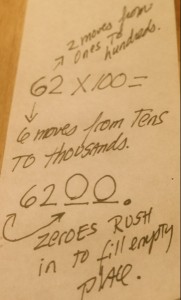



 As Robert tells it, fractions had a good run, and with a 5,000+ year history, they’ve outlived every fad imaginable, including paisley togas and virgin sacrifices. Fractions began their long run with the Egyptians, who utilized them to divide up plots of land and levy taxes. The ancient Sumerians loved fractions so much that they invented the 24 hour day, the 60 minute hour and the 360 degree circle just so they could divide them up into equal pieces really easily: a 24 hour day can be divided into halves, thirds, quarters, sixths, 8ths, 12ths and 24ths (don’t get me started on how easy it is to divide 60 and 360….) You just can’t do that with 10 or 100.
As Robert tells it, fractions had a good run, and with a 5,000+ year history, they’ve outlived every fad imaginable, including paisley togas and virgin sacrifices. Fractions began their long run with the Egyptians, who utilized them to divide up plots of land and levy taxes. The ancient Sumerians loved fractions so much that they invented the 24 hour day, the 60 minute hour and the 360 degree circle just so they could divide them up into equal pieces really easily: a 24 hour day can be divided into halves, thirds, quarters, sixths, 8ths, 12ths and 24ths (don’t get me started on how easy it is to divide 60 and 360….) You just can’t do that with 10 or 100.