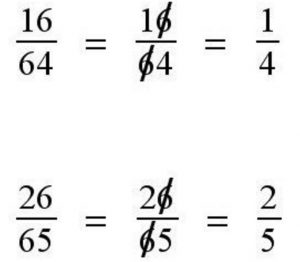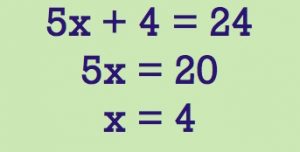I remember one of my earliest memories of teaching math is giving an assignment where 18 had to be divided by 4. A student looked up from his work and stated, “wait a minute, I can’t do this problem. 4 doesn’t go into 18….”

“Well,” I explained, “Actually, 4 is smaller than 18, so it does ‘go in’….”

“No, you know what I mean,” the student continued, impatiently, “it’s going to leave a remainder!”

“Soooooo? What you mean is that 4 does go into 18, it just doesn’t go in evenly.”

My student shook his head and continued on with his work, as if I committed some kind of sacrilegious act of mathematical heresy by having him solve a division problem that didn’t come out evenly. I thought about how limited my student’s knowledge of division seemed to be, and thought I had nothing to do with it.

But I did, because, up to that point, all the division problems in our textbook had come out evenly, so my student (and, no doubt, his classmates) were conditioned to believe that problem with remainders were either incorrectly worded, or that their own answer must be incorrect.

I gave this a long hard thinking and reached the following conclusion: the reality is that most division problems do NOT come out “evenly” and that this should be reflected in the problems we give our students from the very start. In fact, our students should be surprised (or suspicious) when a division problem comes out “evenly,” not the other way around.

Here’s an answer key from a popular site that provides worksheets (name withheld) – it is probably not unlike a division practice activity found in your textbook.

Yikes! A student doing these kinds of problems would get the impression that all long division (which I call “multi-step division” because nobody really agrees on what long division really is….) has no remainders. Now, is that really true?

In the program I direct, we start students on division with remainders from the beginning. We spend a lot of time on interpreting remainders, because, believe it or not, they do matter! The last thing we want is to have a student look at a problem and say, “wait, this doesn’t go into this….”

One of the materials I developed is a set of exercises where a single division situation is given, and the remainder has to be interpreted four different ways. The division problems are “simple,” but depending on the question posed, the remainder can be interpreted in different ways.

Example: spozen you had 28 eggs and you want to put them into cartons that hold a dozen? Depending on the question, it could be 2, 3, 6/7 or 1/3. How so? Well, if the question was “how many full cartons could you fill?” the answer would be 2. If you asked “how many cartons would you need to hold all the eggs?” the answer would be 3. If the question was “What fraction of the eggs will fit into cartons, it would be 24/28 (which simplifies to 6/7) and if you ask what fraction will be left over, the answer is 4/28, which is 1/7th. There are more questions you can ask, but you get the point.

During a recent visit to Munich, I had an inspiration for another activity: in the multi-floor buildings, the individual apartments are not numbered according to location (as in 3A, 3B, which means 3rd floor, apartment A), but sequentially (if there are 20 apartments in the building, it goes 1 through 20.) So the number of the apartment doesn’t tell you which floor it’s on or where it is located.

So here’s the idea: what if you knew the number of floors and the number of apartments on each floor? Using division, you can find the location of each apartment: if there were 20 apartments in the building and 5 on each floor, then you know apartment 5 is on the first floor, 10 is on the second floor, 15 is on the third, etc. But what if the apartment number does not divide by 5 evenly (which it doesn’t most of the time)? Here’s where the remainder is important: if you are locating apartment 6 and you do the division (6 ÷ 5) you end up with 1 r 1; well, the remainder tells you that the apartment is located on the second floor, and not only that, it is positioned on the front left of the building!

I’m always encouraged by writers who advocate for “non-traditional” people going into mathematics and science careers (I just recently did a hard-sell to a Haitian-American accountant on the A train between Columbus Circle and 125th Street. She promised she would call me…), but not all help is really “helpful.” This opinion piece, published in our hometown rag, The New York Times, is a good case in point.

I’m totally down with the author’s opening paragraphs, which points out an interesting paradox: if you are good at one thing, and even better at another, you tend to choose that thing which you are even better at to focus your attentions: if a girl is good at math, but marginally better at language arts, being the rational person she is, the girl will go with what she believes is her strengths. This concept of “relative expertise” (my words) both important and novel, and should be explained to all teachers, so they can give students more choices about where they want to put their attentions. Of course, the author cites a “wide body of research,” but does not cite even a single study or meta-study. C’mon, doesn’t evidence count in writing as much as science?

The second place this piece goes wrong is this statement:

“Unfortunately, the way math is generally taught in the United States — which often downplays practice in favor of emphasizing conceptual understanding — can make this vicious circle even worse for girls.”

You know, I’ve been hearing about this (non) issue for over 30 years, and again and again I’ve asked the person to name a single mathematics curriculum that does not advocate for skill acquisition. Each time I’ve been told, “well, I’ve heard about them….” which is the same technique used to promote the myths of the Loch Ness monster  and something called “compassionate conservatism.” The fact is this: all teachers know that practice is essential to mastering a skill, whether it is spelling or recalling multiplication facts.

The only question is what is the best way to promote this? This is where Oakley goes further off the tracks: her simplistic education view is that acquiring these skills can only be seen as drudgery worthy of a Charles Dickens novel. Um, message from reality: practice can be fun and lead to long term skill acquisition, if done correctly. Conversely, practice done as a series of mindless and “boring, but this boredom is totally good for you” steps can be both detrimental to the soul and actually diminish performance and understanding.

(One person’s idea of “fun.”)

I’ll cite actual examples from “real” curricula that is out there, because that’s what is called “evidence.” TERC’s “Investigation into Numbers, Data and Space,” as well as the University of Chicago’s “Everyday Mathematics” are both held up as curricula that are “light” on fact acquisition by those who are misinformed. The fact is, both advocate for skill acquisition, but instead of doing it in the traditional way, through endless worksheets, they embed practice through a variety of puzzles and games that can be played over and over again, and can easily be modified to remove “obvious” and “learned” facts. Seriously, do students really need to practice multiplying by 0, 1 and 10? 

Along with this, an entire industry of apps has sprung up that promise to help students practice mathematics facts, although I have many criticisms about those as well (and it has nothing to do with whether they are “fun.”) Dr. Oakley clearly has a position to push, but the problem is this: it throws the baby out with the bathwater.

Alternatively, mindless practice, besides being boring (and thus confirming that mathematics is a dull subject where all you have to do is repeat what the teacher showed you), can also be destructive. Imagine a student who has been told to practice multiplying whole numbers by powers of 10 (that is, multiplying by 10, 100, 1,000, etc.) The student quickly picks up that this can be easily accomplished by adding a certain number of zeros to the multiplicand (the first number in a multiplication problem, because these problems always look like “55 x 1,000” and never “1,000 x 55”) and then moving on to the next problem.

All good, right? The student practices a skill, does a few dozen and the skill is tested and then considered “mastered.” Um, not quite: the “add the number of zeroes” property only works with whole numbers! Later in their studies of mathematics, the student encounters “5.9 x 100” and what do they write down? Well, because they practiced and “mastered” this “skill” a few years back, the answer to any reasonably intelligent student is 5.900. And so the teacher has to “unteach” a skill that was thought to have been mastered. 

Finally, please allow me to put a nail in the coffin of any opinion piece that uses PISA data to prop up their case. PLEASE STOP USING PISA DATA TO PROP UP ANY ASSERTIONS YOU HAVE ABOUT MATH EDUCATION IN THE UNITED STATES. PLEASE!

We can go through this hundreds of times, but using PISA data to support an argument is not only intellectually weak, it is downright fraudulent, on the level of “fake news,” but even more so, because it is nothing short of “fake data.” I don’t know where to start, but I think this article sums up the issues pretty well. If Forbes can see why PISA data is useless, then you should as well.

So what is the “solution” to encouraging more girls (and I mean girls of color as well) to go into mathematics and science related fields? The answer is not more practice. One of the answers is to give them more “role models,” including Dr. Barbara Oakley, as well as giving them more opportunities to see that you can be good in both math and humanities and not choose one or the other. This is the life story of Maryam Mirzakhani, an Iranian woman who loved novels as a student and applied her appreciation of storytelling to her work in mathematics. Maybe a better use of our girls time would be to watch Mirzakhani at work, instead of completing another round of boring worksheets.

Dr. Oakley could definitely do a lot to advocate for the cause of girls and mathematics, but her prescription lacks any fundamental logic and her conclusions are not only simplistic, but can ultimately be misinterpreted and lead to another generation of girls who are under-represented in the field of mathematics. 

Addendum: I contacted Dr. Oakley about my concerns, detailing my misgivings about using PISA data as well as conflating “practice” with “fun.” Her response is as follows:

Dear Robert,

Thank you for your insights.

Warmly,

Barb

Here’s an interesting fact for you: in the 2012 vote for state assembly seats in Wisconsin, candidates from Party “A” garnered 174,000 more votes statewide than the candidates from Party “B.” In fact, Party “A” received 53% of the votes in the state legislative races, while Party “B” received 45%, with the remainder going to third party candidates.

Since one of the hallmarks of our democracy is “one person, one vote,” it would be safe to assume that Party “A” also won 53% of the Assembly seats, while Party “B” controlled 45% of those seats. Or at least something close to that, right?

Well, no, as a matter of fact, the outcome of that election was that Party “B” ended up with 60 of the 99 Assembly seats, while Party “A” ended up with 39. To sum it up, Party “A” got 53% of the votes, but ended up with 39% of the seats, while Party “B” got 45% of the votes and took 60% of the Assembly seats, making it the majority party, and ruler of the legislature.

Does something smell a little fishy to you? I hope so.

This crazy district in Alabama ensures one power stays in power. Care to guess the name of that party?

This crazy mathematical outcome is brought to you through the magic of “gerrymandering,” where legislative lines are drawn so that one political party is favored over another. The mathematics of this is not terribly complicated: all it requires is creating districts where all the voters from one political party are either concentrated into a small area, or “diluted” into districts with voters from the opposing political party. This is a practice that has been around since the founding of the United States; it was even practiced by that great patriot Patrick Henry to prevent James Monroe from being elected to the House of Representatives.

This is a small example of what happened in our national election, where the candidate from Party “C” earned close to 3,000,000 more votes than the candidate from Party “X.” If this seems familiar, it’s because the exact same thing happened in 2000 election, when the losing candidate from Party “C” earned over 500,000 more votes than the candidate from Party “R.”

Part of the reason for this is that the concept of “one person, one vote” has always been a fictitious idea in U.S. history, sealed into our Constitution from the founding of the republic when slaves were counted as 3/5 of a free person for census purposes, yet deprived of the power to vote.

States with large slave populations got 60% more representation due to the 3/5 “compromise.”

This meant that states with large slave populations were able to wield far more power than was mathematically possible if only free persons were counted. If you lived in a state like South Carolina, where nearly half the population was enslaved in 1790, then your vote was worth almost twice as much as  other citizens (actually, a free white male with property) who lived in a state that had few to no slaves.

That principle is alive and well in our electoral college system, which gives disproportionate amounts of power to states with very small populations. A person living in state “W,” with a population of fewer than 600,000 people, has twice as much say in our national elections than a state like “NY” with over 3 times the population.

If all this is making you want to pack your bags and move to a “real” democracy, you’re not alone. However, through the power of mathematics, there may be a fix for places like Wisconsin (and many other states as well), where the voters choose one thing and end up with something very different. As this is being written, a major case is moving through the courts which will bring some fairness to the system, so that the majority of the voters will actually get the majority of power. Isn’t that a good thing to maintain a healthy democracy?

Coming soon to the United States of America: Representative Democracy!

On November 21, 2016, a federal judge ordered the state of Wisconsin to re-draw the state districting maps based on a recently developed mathematical measurement called “the efficiency gap.” This is defined as “the difference between the parties’ respective wasted votes in an election, divided by the total number of votes cast.”

To put this into more understandable terms, the statisticians who developed this measurement came up with a number they called “wasted votes.”  These votes come in two forms: the first are “lost votes” that are cast by people voting for the losing party, and “surplus votes” cast by the winning party.  For example, lets say there is an election where five seats are up for grabs. The results for four of the districts is a 57% to 43% win for Party A, while the final district is won by Party B with an outcome of 85% to 15%. Party A gets 4 seats, Party B gets 1 seat. Sounds fair, right?

Not so fast, pal.

Had the districts been drawn differently, the 85% of the votes earned by Party B (a surplus of 34% over the 51% needed to win that district) could have been distributed over the other 4 races, giving Party B a better shot at occupying more seats. By doing a simple calculation, we find that there was an efficiency gap of 40% in Party A’s favor. If the efficiency gap was brought down to a more reasonable 3-4%, the actual outcome would give 2 seats to Party A and 3 seats to Party B, a much more “representative” outcome of the voters’ intentions. By re-drawing the districts so that there are fewer lopsided races like this, we actually end up with a more robust and representative democracy.

For those of you who despair at the state of our nation, it should be remembered that while it was mathematics that got us into this mess, it is ultimately mathematics that will help refine our government so that it is truly representative of the the will of the citizens.

This blatantly political post has been brought to you by SamizdatMath, where you can also find these fine materials that will cause you to think more carefully about our political and economic system:

Interdisciplinary studies at its best: use historical data to analyze the political composition of the United States in 1790!

At look at the recent election: who really was the biggest and boldest liar?

Was the 2016 election really won in a landslide? How common are “landslides,” anyway? A look at the outcomes of our 58 presidential elections, where students calculate percentages, percent of a number in a compelling context.

Explore how the wealth of the US is distributed; you won’t like the results.

And would someone please hit the “follow” star so that I can finally reach 500?

Loyal readers know that Robert, the originator of this blog and the proprietor of the online store of the same name, has a very low threshold of tolerance for bad mathematical materials. His past posts on this topic, which includes “Why Singapore Math Will Not Put the US at the Top”  and “What Bad Assessment Looks Like, Go Math! Style…”  solidly confirms his status as the top curmudgeon for what he terms “the competition to see who has created the worst math curriculum ever.”

While taking a morning walk along the streets of his Free State of Brooklyn last week, Robert happened upon a brand new sealed and complete set of teaching guides for something called “Math 180”, which the publisher’s website describes as follows:

MATH 180 is designed to address the needs of struggling students in grades 5 and up, and their teachers, equally—building students’ confidence with mathematics and accelerating their progress to algebra.

Word Problem: How many mountains of trees had to be pulped to publish just the teaching guides?

I’m going to assume the part about addressing the needs of students AND teachers is an attempt to acknowledge the fact that many teachers of mathematics are unprepared to actually to do their jobs. Mathematics is a technical subject, and unfortunately, many of the teachers who are in the position to educate students in this area are inadequately trained or supported. This is not because they are inept or uncommitted, but because of the low standards of preparation and understanding that we are willing to accept in our schools.

The shameless “experts” who were paid to put their names on this crud.

So Robert schleps home with this box of teaching manuals, which consists of 6 different thick books, a very retro looking CD (remember those?) AND a thick packet of classroom posters, all of which weighs in at just under a fully loaded Mini Cooper. Opening to the “Math 180 Experts” page, Robert finds the usual gallery of “Lead Authors”, “Advisors,” “Contributors,” and the members of an “Educator Advisory Board,” each of whom was most likely offered a nice chunk of change to act as if any of them had any hand in the creation or production of this scheisse.

Robert was impressed at how the people who actually put together this curriculum worked to check off every kind of educational trend, scattering in references to Carol Dweck’s “growth mindset,” to “Universal Design for Learning,” along with “blended learning,” “formative assessment,” and a host of other educational hot topics that probably stimulate the endocrine glands of people who love this kind of stuff. Don’t get him wrong, Robert adores Carol Dweck, and believes that UDL is good stuff, but if you delve a little deeply, you would see that the actual curriculum violates all the precepts that the aforementioned experts would advocate. Oh, and just to make things they didn’t miss ANYONE, they also listed two “advisors,” as well as one “contributor” from Singapore, because we all know that including that semi-repressive city-state’s name in the context of mathematics education will be just the poke textbook adoption committees need in order to sink massive amounts of public money into this cruddy program.

Once you get past all the marketing materials, you see a pretty dull curriculum which uses all the standard models to remediate middle school students who have either fallen behind or were “turned off” by the mathematics instruction they had before. I was especially impressed by the “relevant” word problems the copy editors included. Check out a few of the following:

Because using the words “email” and “video games” in a word problem instantly makes it “relevant.”

If Dave is writing 20+ reviews each week, when will he have the time to do “Math 180?”

Well, we think you get the point: same old “pseudo-content,” same old teacher centered instructivist methodology, same old reward based assessment (you get “badges” if you reach certain levels while using the online learning materials), all gussied up and pre-digested for your use. Okay, we understand that Scholastic, and the marketing agent, Houghton-Mifflin Harcourt YouNameIt, are profit-making concerns and need to return “value” to their shareholders (which probably includes companies like TIAA-CREF, which manages retirement plans for educators), but c’mon, really? You have all these talented authors, advisors, reviewers, copy editors and art directors, and this is the best you can do?

Robert would especially like to castigate the cast of characters who were bought off to put their names and photos in this worthless pile of junk. Okay, we know the teaching profession is not especially well-compensated, but Deborah Ball, you’re a dean at the University of Michigan! We’re sure you get excellent health insurance and retirement benefits, so is it really worth selling your good name to be a pretend “lead author” of something you probably spent a few hours red-penning over your morning coffee? Let’s get real: Scholastic really should have used its budget to create interesting and compelling content, instead of squandering it on empty endorsements, outdated methodologies, fancy graphic design and inept copy editing.

This post was brought to you by the entirely unprofitable concern known as SamizdatMath, and matho-educational syndicate which develops and self-publishes uncompromising mathematics materials for teachers in grades pre-K and above. This particular rant was brought to you by:

Readers, do you live in fear of teaching division to your students? Do you stay awake at night laboring over unique division examples that come out evenly? Do you squirm every time a student looks up and says, “but blach doesn’t go into blah-blah-blah?” Do you drift off into la-la-land whenever a student complains, “hey, there’s a remainder here; what should I do with it?”

If this bothers you, then consider the options of using the duodecimal system, aka “base 12.” In the base 12 number system, you have many more options to give division problems that are “remainder free!”  Yes, now you can strike one less issue off your list: fewer remainders means neater division problems, no complaints about extra numbers and, most importantly, fewer decision to make! With the duodecimal system, you can divide by 1, 2, 3, 4, 6, and 12 without worrying about pesky remainders! Try that with the crummy old decimal system: divide by 3, 4, 6, 7, 8, and 9 and what do you end up with? REMAINDERS! Urgh!

Okay, the world will not be switching away from the base 10 system anytime soon, and remainders are going to be a fact of life well into our collective future. So the question is this: what should you tell your students to do with the remainders that inevitably come from dividing?

a) Do the problem over; all division problems in school come out evenly.

b) Write it as a whole number, and let someone else deal with it.

c) Leave it as a fraction, whatever that is.

d) Leave it as a decimal, so long as it comes out evenly. If not, refer to choice “a.”

e) Round up to the nearest whole number.

f) Round down to the nearest whole number.

g) All of the above.

h) None of the above.

i) Check Khan Academy.

j) It really depends; remainders on division problems are highly contextual.

Well, if you know my style of writing, you know the answer is “j,” but given how many teachers treat math as a set of “rules” to be obeyed,  it is most likely that a student will choose a, b, c, d, e and/or f. Harumph….

The simple fact is this: most division problems do not come out evenly, and why we persist in giving students a steady diet of problems that leave no remainders is beyond my comprehension. The presence of remainders should not be seen as an “oddity” when dividing; rather, we should teach it as one of the essential properties of how division works: most numbers do not go into other numbers evenly, or even once (the “bigger into smaller” issue, which I’ll cover in another rant…), and yet we persist in giving students a steady diet of division situations which work out evenly. Therefore, if we give word problems where remainders are the exception, rather than the rule, our students are not going to have strategies for dealing with remainders.

Consider the five problems shown below, all of which have remainders, all of which require different interpretations.

In the first problem, the remainder gets discarded, while in the second problem, the remainder should be written as a decimal. The third problem is best left as a fraction, the fourth problem needs to be rounded up and the fourth problem doesn’t even need division at all: just multiply 7 boxes times 6 donuts per box and you end up with 42, which is larger than 39. Do I have to do everything for you?

Teachers of mathematics, we have to wise up! Give your students lots of word problems where the divisor doesn’t gozinta the dividend evenly, and have them interpret the meaning of the remainder. It’s either that, or push for decimal reform and invest in base 12 calculators!

This post has been brought to you by the hardest division assessment you could ever give to a student who believes “I know everything there is to know about division.”

Hand your students a calculator and watch their brains sizzle! Comes complete with teaching tips, answer key and suggestions for activities that you can do in the classroom.

I started teaching waaaay back in 19, wait for it, 84. I was a much younger man back then, and while I thought it seemed like a good way to earn a living, I had no idea the actual “craft” would engage me for more than three decades. Back then, I honestly believed that it was all about teaching a few skills and then testing to determine how much my students remembered. In that sense, I believed that teaching was like running a series of controlled experiments: teach, test, teach, test….

As I struggled through the first year, the head of school, with whom I found myself at odds with, offered me a book called “The Art of Teaching” by Gilbert Highet, which actually proved to be my undoing when I attempted to implement the ideas expressed. I had actually read another book about teaching when I was 14 years old, 36 Children by the wonderful Herbert Kohl, which got me thinking about teaching as a force for social justice. My first year was rough, but it was then during that year that I understood, I was born to teach. I also learned that the idea of “teach, test, teach” just was not the essence of the profession. There was much, much more to learn and do….

Two definitive books on teaching; both were “borrowed” and never returned to their owners.

Flash forward 32 years, and here I am, back where I started: a new year, new thoughts about teaching, and new things to do. I stopped in to visit the lovely teachers who rule the 2nd grade (or, what we call the “7/8s”) and what did I find but a lovely activity based on Eric Carle’s beautiful story, Rooster’s Off To See The World. As with all of Carle’s books, the illustrations are engaging, and the story works on many levels – it is nominally about a group of animals out for adventure, who ultimately opt for the “creature comforts” of home. At the same time, it is a counting book, designed to introduce the young to numbers and patterns. The teachers had posed a problem to the students: if there are 14 animals off to see the world, how many legs would they have? This is not an easy question, because some have 2 legs while others have 4, and there are 14 numbers to keep track off, which is no easy task for a child (or even an adult.)

I looked at the book very carefully and decided for myself, well, this is a wonderful book and the idea of keeping track of legs on animals is a provocative one for young children to do. But I also thought that turning the tables on the activity, that is, giving young children the chance to ask questions of one another, would be a fun and engaging way to get them to interact with one another.

There was just one problem with this plan: there is a great deal of variety in the legibility and spelling of 2nd grade children, as well as their motor skills in writing out questions. I wanted them to create problems quickly, so that they could focus on the mathematics, rather than letter formation, sentence structure, grammar and punctuation, to name a few elements of literacy. I also didn’t want to get into trouble with the publishers of Mr. Carle’s book due to copyright infringement, which meant staying away from his imagery and characters.

Instead of rooster, cat, frogs and turtles, I decided to simplify the activity by using only 3 animals. At the same time, I wanted to vary the number of legs on the animals, that way I could have more combinations: so I used an ostrich (2 legs), wombat (4 legs) and ants (6 legs.) I also think that ostriches, wombats and ants are interesting animals, don’t you?

With those decisions made, I designed three different stamps that students would cut out to make their questions: instead of writing out long sentences with stories, I envisioned them cutting and pasting combinations of the animals, with the simple question “How many legs?” printed underneath.

Well, this seemed like a promising start, but why stop at just addition? Since subtraction is also a good topic, why not create a simple problem that involves comparing the number of legs?

and while we’re at it, why not add something even more interesting and open ended?

Oh, this is muy muy fun, and if you don’t agree, well, you just don’t know what the definition of fun happens to be….

To add finishing touches to this activity, I thought about what could be done to get kids to think more carefully about how they create their problem, as well as offering a means to initiate discussion of their solutions. Which is why I created a separate sheet where they could make an answer key for the question they asked, as well as offer a “clue” about how to approach solving the problem:

Isn’t this beautiful? Well, that’s not all, because I added one more innovation which I think I may use on every single activity I make in the future:

Do you get what I’m attempting to do here? Instead of putting the name of the students at the top of the paper, which is what you do when you start something very monotonous (like take a test or apply for a learner’s permit at the DMV), I thought it would be much more important that a student “sign off” on their work after it has been created. Much like no artist every signs a work before creating a sculpture, painting or dance piece, a student should not sign off on a piece of mathematical thinking until after it has been completed. This allows the student to feel a sense of process and completion to what they have done. I feel very inspired by this tiny little change, and I hope you’ll use it as well.

The scariest thing I can imagine about being in my profession is doing the same thing year after year. Working with a staff of vibrant educators means that I always have the opportunity to do more and more, as well as refine what I’ve already done, AND share it with the rest of you. At 32 years in, I’m still feeling young…

This post has been brought to you by…..

Robert has a new Pinterest board called Fraction Teaching Mistakes where be trolls through the wide world of what passes for “good” mathematics materials and comments on the inherent flaws in one activity or another. Some he objects to because they hide the underlying beauty and logic of mathematics through “magical thinking” (for example, “butterfly methods” for comparing fractions), while at other times he finds very rigid representations (“will we ever see the end of fractions represented as pies?”  he often laments…), not to mention information that is just plain wrong (2/5 x 1/3 = 11/15?)

Materials like this focus on “peripheral” activities like coloring in shapes. Avoid at all costs!

One of the things that really irks Robert are math activities that focus too much attention on peripheral activities, like coloring, cutting and pasting. These projects look very pretty when completed, but unless the teacher’s specific goal is to create a work of art, they are pretty much a waste of time.

At the same time, it could be useful to take a break from using pencils and screens to do math, and cutting and pasting are good for motor skill development, so why not let the kids have a change of pace? How can we design a cut ‘n paste activity that makes the most of a student’s limited time in math class, without unduly devoting the majority of time on scissors and glue? How can we maximize the amount of thinking that will take place?

One thing that has to be considered is on designing the “cut outs” so that it can be cut out efficiently and with a minimum of wasted paper (which is why Robert objects to the use of most “cutesy” clip art that routinely gets inserted into many materials.) Check out the “cut outs” used in a 3rd grade activity below:

There are three reasons to object to this: the first is that it is difficult for young children to cut out, what with the individual pieces and rounded corners. The second is that there is a lot of white space between the different “cut outs,” which mean that it is a waste of paper. Third, since there are more symbols than actual problems, the students will be cutting out materials that are unnecessary. While the activity may be useful, this is seriously bad design. After making all the cuts (there are 13 separate pieces, at 4 cuts per piece, which is 52 different cuts, not to mention the time rounding out the corners) how much time do you think will be left to “do math?”

Robert approached the “cut ‘n paste” activity and redefined it as a design challenge, seeking to have the most “work” with a minimum of cutting. Here’s what he came up with:

What you’ll notice is that there are no rounded corners to trim, and that almost every piece is adjacent to another, so that one cut actually trims 2 separate pieces. The 24 pieces can be separated from the main sheet with two easy straight cuts, and then laid on top of one another two at a time to minimize cutting. The fifth graders who did this activity typically were ready to place their pieces in fewer than a dozen “cuts,” which look about 3 – 5 minutes. In addition, there was a minimum of paper waste, as the activity only left behind two small squares of paper and 2 thin strips.

Since Robert is a calculating guy, he figured out that there was less than 5% wasted paper, and 90% less cutting than other activities of this type. With less time on cutting, the students had much more time to think about much more important things, like “if 1/7 is .142857 on the calculator, and it’s rounded off to .142, why isn’t there one on the sheet?”

This post has been brought to you by…..