I work with a student who attends a school for children with special needs. He’s a very nice kid who is very eager to do well in math, even though it presents many challenges to him. His parents decided to meet with the math teacher with whom he would be working this year, and she mentioned that the students would be doing a unit on problem solving focusing on the “key words” approach to answering word problems.

I was shocked. No, strike that: shocked. I was astonished! I haven’t heard of anybody using this approach for as long as I’ve been working with teachers (which goes back to the previous century), and I had thought that after it had been died a complete death after being thoroughly discredited. How was it possible that this approach had risen to mis-educate a  new generation of students?

One of the “keyword” anchor charts that lurk on Pinterest

I’ll show with just how bad an idea it is to teach problem solving with keywords by using a single example: I had 5 apples in my basket on Monday. On Tuesday I increased the amount of apples so now I have 7 altogether. How many apples did I add on Tuesday?

If the student had been the victim of a teacher who used the “key word” approach, then by following these directions, he would have been absolutely correct to add 5 and 7 to get 12 apples. After all, the “key word” altogether is used in the question, as well as increased and added. The question does not contain any of the subtraction keywords, which includes difference, take away, left, still, minus and take away.

Some teachers might argue that this is a “gotcha” question, but this is not the case. In fact, it is a question that I would hope a 3rd grader who has a grade-level understanding of English would be able to turn into an equation and solve. The “key word” technique is a kind of hunt & peck approach to reading and interpreting word problems, and it results in students performing the wrong operation on anything but the most obvious problems. Am I crazy, or is this a seriously bad way to teach problem solving?

So what should we be doing in the classroom instead of teaching “key words?” The best approach is to do things that actually require thinking, like having the students build models that will help them solve the problem. Mathematicians do this all the time; why not have students? These models could be physical or written, but regardless, they are models and they help students actually “think” about the meaning of a problem.

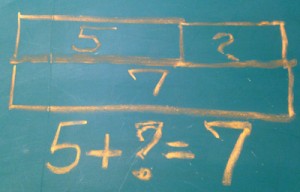
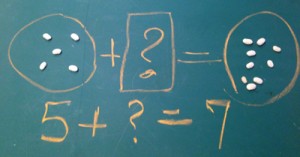Both models to the right can be used to solve the problem described above. The top one uses a “bar model” which is attributed to the Singapore Math program, but was actually developed by W.W. Sawyer over a half-century ago. By comparing the part (the 5 apples I had on Monday) with the whole (the 7 apples I now have on Tuesday), I understand that I am “adding” on to 5 until I get to 7.

The second model does essentially the same thing, but uses manipulatives: the child “acts out” the timeline of the problem by putting 5 beans in the first circle, showing that some apples are being added, and the result is 7.

Please, please don’t download or hang this chart in your classroom.

I don’t know who came up with the idea for using “key words” when teaching children about problem solving. It’s a seriously bad idea that somehow made its into the everyday practice of misguided teachers around everywhere. It substitutes comprehension for shortcuts, and disengages children from the actual practice of what mathematical thinking look like. I can guarantee you that there is not a single economist, biologist, chemist, statistician or anybody working in the field of mathematics who solves a problem using this method. Why would we teach it to our students?

Note: this rant has been brought to you by none other than Robert M. Berkman, proprietor of the SamizdatMath curriculum collective. If you are interested in including visual approaches to problem solving, try out this set of algebra problems which promote algebraic reasoning without the use of nonsensical “key words!”

I have an online “colleague” who makes no bones about the fact that she hates math. She’s expressed this opinion in numerous message threads on a community board to which we both post. She works in science education, and is about the most civil and respected voice as one is likely to encounter on these kinds of open forums. If there is one vice this person possesses (and I’m quite sure it is only this), it is that she continually professes, quite seriously and earnestly, that she hates math.

I don’t think she’s telling the truth. I believe it is impossible to “hate” math. Saying that you “hate math” is the equivalent of saying “I hate music,” or “I hate food” or “I hate animals.” Okay, everyone dislikes a certain style of music (those 12th century Gregorian Chants are not my favorites, truth be told) and it is possible to have negative reactions to things like okra when it is slimy instead of crispy, and yes, nobody likes lice, but really, a generalized statement declaring a hatred of math is just not possible.

Mathematics is an incredibly diverse field of study, and it encompasses so many different ways of analyzing and solving problems that a blanket statement like “I hate math….” cannot possibly make any sense. In fact, it is so nonsensical that it would be equivalent to declaring a hatred for thinking and feeling.

I can confidently say this, though: there are times when even those of us who know and enjoy mathematics find it either boring or frustrating or some combination of the two, but we also recognize that this this is not unique to mathematics. Whether you are conducting a scientific experiment or producing a blockbuster movie, there will always be extended periods of boredom and frustration. There’s nothing wrong with this, and I can’t imagine that anybody would discredit an entire activity based on this pervasive reality.

How could you possibly hate this dish?

So here’s my take: it’s not that my friend “hates math.” She only thinks she hates math. The journey to loving math could begin with modifying her blanket contempt for mathematics to something as simple as “I hate math when….” After all, you can hate okra because it’s slimy, but when it’s flash fried in a cornmeal crust, well, that’s an entirely different matter….

Note: this posting has been brought to you by my online store, where you can find this  78 page collection of activities designed to facilitate number sense using different individual coins, as well as in combinations of 2, 3 or 4 coins. The guide also has an extensive preface describing the different types of number sense that needs to be developed at different grade levels.

The Samizdatmath Library

Every Thursday morning for the past 5 years I’ve been meeting with a 4th grade class to work on a variety of “puzzlas” to stretch their mathematical thinking. I pull these puzzles from a variety of sources, which is not hard as I have a library of math materials that I’ve been collecting for over 30 years. Truthfully, I don’t know if I’ve had an original mathematical thought in my life, as my library provides more than enough inspiration to cover me for several lifetimes.

Every once in a while, an interesting puzzle comes across my desk and this puzzle inevitably leads me to start looking at the problem in a bigger way. That is, the specific puzzle leads to a much bigger question. Such was the case of the  problem below:

On the face of it, the problem has a single unintuitive answer which requires constructing a set of floor plans for 4 apartments that no one in their right mind would want to live in. However, it does beg a bigger question: suppose we got rid of the kitchens and bathrooms, and just had to divide up the square into 4 equal sections of 9 tiles each where each shape was congruent?

I started with the simplest solution possible: 4 squares of 9 squares each. I then started by moving one tile over from each of the squares:

Moving a single tile, as is done to create tesselations, creates new solutions to this puzzle.

I’ve been working on this puzzle for the past 8 months and have come up with over 40 different solutions, but my fear is that I’ve missed out on some. Here’s what the results of my research looks like:

….so here’s where you come in, dear teacher: visit my online store and you can download this activity for free! Print it up, try it out with your kids and let’s see if they can come up with variations that I have yet to discover. I’ll publish them here and then submit the results to some mathematics journals to see if we can get it published. Let’s get kids involved in making mathematical discoveries and show them that far from being a dead subject where everything is known, mathematics is alive and quite well.

Lovely place for a school, no?

…she would definitely do this activity.

It was back in the late 90’s (remember them?), and I was working in a school located in a nondescript part of Brooklyn. Whereas most schools seem to be located “in” a neighborhood, this one defied classification: to the south was Green-Wood Cemetery, 248 bucolic acres of greenery which holds the final remains of everyone from the composer Leonard Bernstein to the notorious artist Jean-Michel Basquiat. The north side of the building overlooked the Prospect Expressway, a 6 lane highway which funneled traffic into central Brooklyn; to the east and west, the school was bounded by auto repair facilities and a garage where old bed springs were recycled. Depending on which corner of the building you were standing, you could be in four different neighborhoods.

I was teaching 8th grade, 5 classes, 30 kids per class: they were 75% Hispanic, with families from all over Central and South America, as well as various Caribbean islands. The rest were immigrant families of Asian and West African heritage. Their only commonality was that they were all desperately poor and came from semi-intact homes. One of my favorite students, a very cheerful 12 year old kid named Angel, disappeared for 6 weeks after he was put into foster care when a neighbor turned in his mother for leaving him home alone while she went shopping down the street. He returned to my class, and I continued to follow-him as he delivered food in my neighborhood while attending high school and college. I always gave him big tips, even when the kitchen got my order wrong.

This was not the most motivated group of students and they were several years below grade level in mathematics. Each day I committed myself to creating an activity that would draw students in, to make learning mathematics “irresistible.” I was thinking about my introductory lessons about geometry and started playing around with the idea of something in between a compass and a protractor: the compass allowed one to move around in a circular motion, creating angles of various sizes, while a disk would mimic the measurements found on a protractor:

The design couldn’t be simple enough: 2 arrows and a circular disk, a couple of holes and a paper fastener. I introduced the lesson by explaining that mathematics is about classifying and measuring. We discussed how there are different types of numbers (odd, even, primes, composites), shapes (triangles, quadrilaterals, pentagons, etc.) and operations (addition, subtraction, multiplication and division.) We also discussed all the different ways you can measure different properties of a shape, including length and volume.

With this “preview” finished, I give my students free reign to move the arrows around, and try out the device to measure and sketch angles they find around the room, as well as on the hallway. I keep a stack of old magazines in my classroom (which is why the librarian is my best bud) where they can look for pictures of things with interesting angles. My students record these angles using a ruler to make the rays. At the end of 20 minutes, we have a pretty good collection.

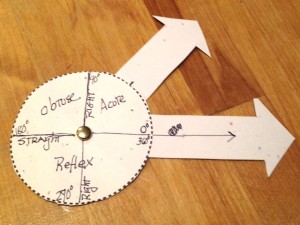
I then take the pictures and sort them into three groups: those with acute angles, those with obtuse angles and those with right angles. I intentionally leave out straight, reflex and zero angles because they are not “typical” angles. I ask my students to describe the difference between the three types of angles, and as they do so, I have them start labeling their “angle finders” with the angles and their names. One of the things you’ll notice in the photo above is that “right” angles are labeled twice, both as 90˚ and 270.˚ I do this because I want to reinforce the idea that a “right” angle has nothing to do with the direction an angle faces, but with the degrees between the two rays.

Incidentally, the term “right angle” is derived from the practice of carpenters to build everything from door frames to cabinets using 90˚ angles; since this angle was so common in their work, they referred to it as a “right angle.” This is an important linguistic distinction to make, as our students are too often tripped up by the difference between the vernacular and technical language of mathematics.

As we continue to classify angles, I also have students put in the “landmark” angle measurements, which includes 90˚, 180˚, 270˚ and 0˚/360˚. It is important that students “see” that there are two types of uncommon yet still important angles: that is, that a straight line can be classified as a 180˚ angle and that a single ray can also be thought of as the overlap of two rays pointing in the same direction, creating either a 0˚ or 360˚ angle. Even those these are “exceptions,” I find it critical to point these out, as mathematics is filled with all kinds of “exceptions” and these “exceptions” are no exception.

There are many other activities that go along with this little gadget (you can purchase the template for this device as well as a set of clue cards that incorporate problem solving into this activity), and it’s been enormously helpful in keeping my students motivated and proficient in their understanding of geometry. Check it out!