Robert has been accused of being a serious badass when it comes to mathematics, most likely because he is very adamant about “getting things right.” According to Robert, “there are no shortcuts to understanding,” when it comes to understanding math, but if you look at the materials that are being posted on the web these days, you would believe that manipulating numbers is nothing more than memorizing a dozen or so “rules.” So when this poster showed up on Pinterest (luckily the link to the miscreant was not included), Robert lit’rally blew a gasket:
Would the teacher responsible for this please step forward?
Where does one begin to explain all the problems with this?
The beginning part of this is not all bad: true, multiplying by 2 is also the same as doubling, and yes, you could double a double to multiply by 4. But really, do you think there are a lot of 8 and 9 year olds who can double a double a double? You can almost see the smoke coming out of little Hudson’s ears as he attempts to double 8 three consecutive times: 8 + 8 = 16, 16 + 16 = 32, 32 + 32…. wait, where was I?
Things only get worse as you get further down the chart: yes, multiplying by 0 always equals 0, but does a child really need to memorize this fact? If the student understands the meaning of multiplication, then reciting “times zero = zero, zilch, nada….” and “times 1 = the other factor” is just nonsense. These are essential features of our number system that require understanding, not memorization: times 0 is the “zero property of multiplication,” and times 1 is the “multiplicative identity.” Yes, the word “multiplicative” is a mouthful for a young child, but this chart totally ignores the totally interesting properties of 0 and 1.
But the real howlers are multiplying by 10 and 100. The “adding zeroes” shortcut is incredibly wrong and will only lead to misconceptions the following year when the student learns about multiplying decimals, when he will end up writing down the following:
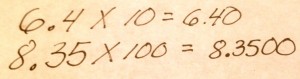
Follow the chart and this is what you end up with…
Make no mistake, this error will not go away in 5th, 6th or 7th grade. In fact, the idea that you multiply by powers of 10 (whether that be 10 or 100 or 1,000 or 10,000 and onward….) by “adding zeroes” is a hard one to shake at any age.
Robert says this: STOP TEACHING ADDING ZEROES AS MULTIPLYING BY POWERS OF TEN!
What should we do instead? Show students that multiplying by 10, because we are in a base ten system, “pushes” all the digits over one place to the left, and that zeroes “rush in” to fill those places that are left empty….
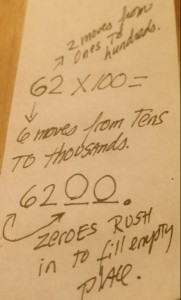
The “right” way to multiply by 10s and above…
The beauty of teaching multiplication by powers of ten this way is that it will always work! It will work with whole numbers, negative numbers, decimals, irrationals, rationals, you name it, it will work!
This post has been brought to you by this guide to teaching place value, from which it has been excerpted:
C’mon, you know you want it….