Robert stops in to see K, the sixth grade teacher, who is twelve kinds of awesome and always quick with a witty phrase (it was from her where I learned to say “for all shits and giggles….”) K looks tense. Robert opens with a corny joke , but she isn’t having any of it.

She plops open her CMP III tome, and points to the chapter on dividing fractions. Robert is thrilled and excited, K not so much.

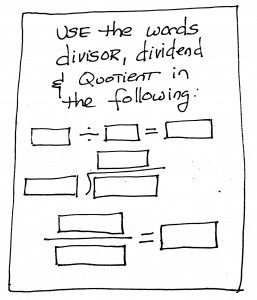
“I thought I would start by writing the definitions of dividend, divisor and quotient on the board and having them copy it down.”

Dear Lord, NO!!!!!!

A pretty good “do now” to review division vocabulary

Robert pulls out a sheet of scrap paper and scribble down the “do now” shown on the left, explaining that her class learned these words in 3rd, 4th and 5th grade, and she really doesn’t need to use more time “defining” these words.In fact, she could probably lead a pretty lively discussion asking the students to define these terms for themselves.

Which gets me to one of Robert’s major issues in teaching: it is 2015 and the era of copying off the board is over. Really over. We should not be writing down definitions on the board and asking kids to copy them down. Repeat: WE ARE NOT RUNNING A SECRETARIAL SCHOOL!

What not to put on the board…..

This is not to say that definitions have no place from the math class, but the danger is this: if you write down definitions on the board and ask kids to copy them down, you are wasting time on a low level skill, time that could be used to do something much more interesting, like discussing what is the meaning of a “dividend” or what would happen to the quotient if the divisor was larger than the dividend. Here’s something Robert did while “guest teaching” a 5th grade class a few weeks back:

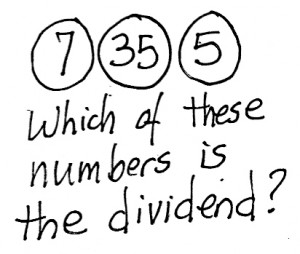
One way to wake up a boring division lesson….

As they say, “you wouldn’t believe what happened next!” A few impulsive students (all boys, as usual) rolled their eyes and called out “35! 35!,” which is exactly what he wanted to happen. However, among all these students who had only a superficial understanding of division, one girl shook her head. “It’s a stupid question!” she explained, “any of those numbers can be a dividend. You could write 7 ÷ 35, 5 ÷ 7, and 35 ÷ 5. The size of the numbers means nothing, so any of the three could be a dividend!”

All of which led into a very interesting about what the “function” of a dividend is, which led to even more insights into the relationship between divisors and quotients.

Later in the day, Robert bumped into “K” getting lunch. “So, how did it go?” he inquired. “Oh, it wasn’t the worst thing I ever did….” she replied.

Wise educators who liked the post above, also put this in their shopping cart:

Read this and learn 12 more ways to get division right in your classroom!