Robert always seems to be obsessing about some aspect of his work, and the last few weeks he has been an absolute veytik in der tokhes because he’s discovered something called “invariance.” He points it out to his students, quizzes his teachers on it, and has taken to philosophizing about it at the dinner table. Even on New Years Eve he couldn’t leave it alone: “You know,” he opined, “I don’t know why we purchased these cruddy plastic champagne ‘glasses’, because the taste of champagne is invariant with respect to the type of container from which it is sipped.” Well, pardon moi!
But since you’re still reading this, you might as well stick around, because this actually is relevant for your teaching practice, and at worst, it would probably make you seem a lot smarter when talking to your supervisors, colleagues or the people you meet at parties who make snarky remarks about “only being a teacher.” If there’s one thing Robert loves is asking a hot shot attorney, “yeah, well, if you’re so smart, tell me, how would you teach invariance to a 5 year old?” and then watch as he takes a gulp of beer and 23 skidoos towards the corn chips.
Okay, here’s the 411 on “invariance” and why you’re going to see mathematics in a whole new light once you “get it.” Eventually, Robert is going to complete his master opus on this topic and then you can buy it at his store, but for now we’ll just dip our toes in the water and leave you with a few questions. But I’m not going to give you a “textbook definition,” because a) that’s boring, b) that’s not the best way to define a concept. Instead, I’ll give you a few examples, and you can work it out for yourself:

“The number of objects in a group is invariant with respect to the order in which they are counted.”
Now you all know that, because our man Piaget described that as one of the earliest forms of mathematical knowledge children exhibit, and which you’ve no doubt observed time and time again. Invariance shows up over and over again in mathematics education. Here’s another example:

“The sum of two groups of ocelots is invariant with respect to the how the ocelots are distributed between the two groups.”
Are you getting the idea? Basically, the concept of invariance shows up whenever we think to ourselves “it makes no difference if….” Robert loves to use this with his first grades when he hands out materials that comes in different colors. “Okay, these geometric shapes come in red, blue and green, but the underlying function of these materials is invariant with respect to their color,” he’ll say, followed by, “can someone just translate what I just said?” The first time he tried this out, a little girl raised her hand and said, “What that means is that you get what you get and you don’t get upset.”
Less we think that this is just something that shows up in the early childhood years, let’s look at an example from the upper elementary grades:
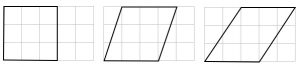
The area of a parallelogram is invariant with respect to the measurement of the base and height.
The above insight came to Robert while observing a student work on one of these cruddy worksheets that a teacher had unfortunately downloaded from the interweb. He asked the student whether it was necessary to re-calculate the area of several triangles which had identical bases and heights, to which she shrugged her shoulders and replied, “I guess so; they’re all different shapes….”
Want to see where this is going in the upper grades? Sure thing: according to Robert, show him a student who is having trouble with solving algebraic equations, and he’ll show you a student who is struggling with the concept of invariance:
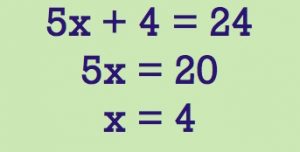
The equivalence of an algebraic equation is invariant with respect to whether the two sides have the same amount added or subtracted, or are scaled by the same factor.
If you’ve been following Robert for any amount of time, you’ll know that helping teachers find a “theme” that carries over from year to year is an important aspect of his work (as well as giving young children brain-busting unsolvable problems….) But if you understand even a little bit about these underlying themes, it will make you a better teacher.
Your Assignment: What mathematics topic are you teaching right now to your students? Do you see the concept of invariance showing up in that topic? How would it help your students better understand the mathematics that they’re learning?
This post has been brought to you by SamizdatMath. Yes, we want to sell you stuff, but our stuff doesn’t keep your students’ busy or look cutesy. Our stuff actually makes your kids “think!”

Textbooks don’t teach concepts, but if you read this and implement all the techniques, you sure will!
