Lovely place for a school, no?

…she would definitely do this activity.

It was back in the late 90’s (remember them?), and I was working in a school located in a nondescript part of Brooklyn. Whereas most schools seem to be located “in” a neighborhood, this one defied classification: to the south was Green-Wood Cemetery, 248 bucolic acres of greenery which holds the final remains of everyone from the composer Leonard Bernstein to the notorious artist Jean-Michel Basquiat. The north side of the building overlooked the Prospect Expressway, a 6 lane highway which funneled traffic into central Brooklyn; to the east and west, the school was bounded by auto repair facilities and a garage where old bed springs were recycled. Depending on which corner of the building you were standing, you could be in four different neighborhoods.

I was teaching 8th grade, 5 classes, 30 kids per class: they were 75% Hispanic, with families from all over Central and South America, as well as various Caribbean islands. The rest were immigrant families of Asian and West African heritage. Their only commonality was that they were all desperately poor and came from semi-intact homes. One of my favorite students, a very cheerful 12 year old kid named Angel, disappeared for 6 weeks after he was put into foster care when a neighbor turned in his mother for leaving him home alone while she went shopping down the street. He returned to my class, and I continued to follow-him as he delivered food in my neighborhood while attending high school and college. I always gave him big tips, even when the kitchen got my order wrong.

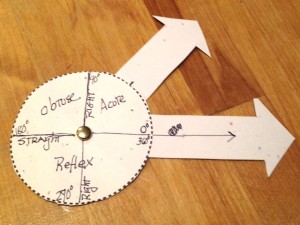
This was not the most motivated group of students and they were several years below grade level in mathematics. Each day I committed myself to creating an activity that would draw students in, to make learning mathematics “irresistible.” I was thinking about my introductory lessons about geometry and started playing around with the idea of something in between a compass and a protractor: the compass allowed one to move around in a circular motion, creating angles of various sizes, while a disk would mimic the measurements found on a protractor:

The design couldn’t be simple enough: 2 arrows and a circular disk, a couple of holes and a paper fastener. I introduced the lesson by explaining that mathematics is about classifying and measuring. We discussed how there are different types of numbers (odd, even, primes, composites), shapes (triangles, quadrilaterals, pentagons, etc.) and operations (addition, subtraction, multiplication and division.) We also discussed all the different ways you can measure different properties of a shape, including length and volume.

With this “preview” finished, I give my students free reign to move the arrows around, and try out the device to measure and sketch angles they find around the room, as well as on the hallway. I keep a stack of old magazines in my classroom (which is why the librarian is my best bud) where they can look for pictures of things with interesting angles. My students record these angles using a ruler to make the rays. At the end of 20 minutes, we have a pretty good collection.

I then take the pictures and sort them into three groups: those with acute angles, those with obtuse angles and those with right angles. I intentionally leave out straight, reflex and zero angles because they are not “typical” angles. I ask my students to describe the difference between the three types of angles, and as they do so, I have them start labeling their “angle finders” with the angles and their names. One of the things you’ll notice in the photo above is that “right” angles are labeled twice, both as 90˚ and 270.˚ I do this because I want to reinforce the idea that a “right” angle has nothing to do with the direction an angle faces, but with the degrees between the two rays.

Incidentally, the term “right angle” is derived from the practice of carpenters to build everything from door frames to cabinets using 90˚ angles; since this angle was so common in their work, they referred to it as a “right angle.” This is an important linguistic distinction to make, as our students are too often tripped up by the difference between the vernacular and technical language of mathematics.

As we continue to classify angles, I also have students put in the “landmark” angle measurements, which includes 90˚, 180˚, 270˚ and 0˚/360˚. It is important that students “see” that there are two types of uncommon yet still important angles: that is, that a straight line can be classified as a 180˚ angle and that a single ray can also be thought of as the overlap of two rays pointing in the same direction, creating either a 0˚ or 360˚ angle. Even those these are “exceptions,” I find it critical to point these out, as mathematics is filled with all kinds of “exceptions” and these “exceptions” are no exception.

There are many other activities that go along with this little gadget (you can purchase the template for this device as well as a set of clue cards that incorporate problem solving into this activity), and it’s been enormously helpful in keeping my students motivated and proficient in their understanding of geometry. Check it out!