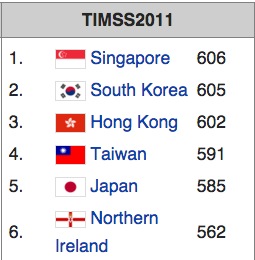
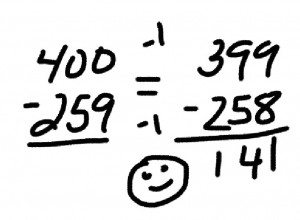Louis C.K. aside, the Common Core State Standards (which Robert dubbed “CoCoStaSta,” because it sounds a lot more fun that “CeeCeeEssEss”) has generated a lot of gosh-awful math lessons that really should never have seen the light of day. But that’s the nature of the beast, isn’t it? Tell someone they have to learn something, and someone will come along and write a lesson plan that will feature some really bad pedagogy, featuring bad raps , confusing worksheets, and, let’s not forget, lots of graphics dripping with cute.
So Robert I found himself a challenge when a teacher friend from Maryland emailed him a request to help develop a super-boffo lesson plan to impress the grand-high-mystic-rulers administrators at a charter school at which he was applying for a position. Now, there are not a lot of things Robert finds more loathsome than Robert is no fan of charter schools, which he views as a way for private companies to steal public money, but he figured if this guy could get his foot in the door, he would find out how awful the whole sitch is and then skedaddle as soon as he could. Meanwhile, perhaps he could build his chops a bit, and Robert could design something cool under the name of CoCoStaSta.
When asked for the topic, it turned out to be the oddly specific “Use addition to find the total number of objects arranged in rectangular arrays with up to 5 rows and up to 5 columns; write an equation to express the total as a sum of equal addends,” which, it turned out, was CoCoStaSta OA 4.2.8.33.PDQ.F#ck, or something of that nature.
Incredibly enough, Robert found this might be a pretty good and even valuable idea for a 2nd grade lesson, so he started thinking about ideas for representing arrays. The first challenge was this: how do I help my students develop the concept of an array? Since Robert is somewhat of an authority on this matter, the challenge wasn’t too great. He would give diverse examples of arrays, as well as “non-examples” of arrays to help my students understand their “critical features.” Here’s what he came up with:

A concept card which shows diverse examples and non-examples of arrays.
Teachers typically get very little training in concept development, which means that they end up never actually developing these important ideas, resulting in “brittle knowledge” among their students. In fact, dear reader, this has happened to Robert himself. He recalled many, many years ago, when Robert was still learning the art of math teaching, after teaching what he thought was a comprehensive lesson on arrays and multiplication, a student come up to him at the end of class and ask, “Mr. B., what is an array?”
What you’ll notice is that Robert uses diverse assortments of examples, which included shapes, rectangular tables, and a set of eggs. He also made sure that the “superficial features” were also diverse, by making them different colors and changed the color and orientation of the stars and eggs, so that students understood it was the arrangement of the entire set, not the individual members of the set that make up an array. Compare this to the examples that you regularly see published in those cruddy textbooks:

Textbook examples of arrays promotes misconceptions by not showing that the individual elements could differ.
With this out of the way, Robert was ready to create the actual activity. This meant thinking of a “compelling context” that would be familiar to a 2nd grader, without being cute or condescending. If you’ve been reading my posts, you know that Robert hates, hates, hates dislikes materials that go overboard on “cute.” I know there are teachers out there (the vast majority of whom also post selfies of their pets on the Facebook or Instagram) who believe that cute = motivational, but I can assure you that while cute is fun for you, most kids don’t really care. I’m all for creating materials that are motivating, but I can assure you it doesn’t come from big eyes and little noses.
So Robert went with something tangible and familiar: eggs. The context is compelling because it creates opportunities to discuss a larger issue beyond arrays: the fact that eggs are packaged a certain way for practical reasons. That is, in which of these arrays do you usually find eggs sold?
Why are dozens of eggs packaged in some ways and not others?
With my context ready, Robert was set to create the rest of the lesson: begin by defining the concept, giving a compelling and familiar context, then going into the nuts and bolts of the lesson. This meant making sure that to take care of a lot of other matters. For example, there is the matter of how you write an equation. For many children, all equations take the form of “X operation Y equals Z,” which is entirely unfortunate, because it means that many children don’t actually know that an “equals sign” actually means beyond “put the answer over here.” This is why Robert made sure to do things like this:

Children need to see that the equals sign can go on either “side” of the equation in order to develop a strong concept of equivalence.
Again, since concepts and misconceptions are important when designing materials, Robert makes sure to use the lesson as a vehicle to reinforce the idea of equivalence, because while we can assume that our students understand what an equal sign means, it’s not always the case.
It is also the case that many students don’t understand (because they get cruddy examples) that arrays can be read from right to left or top to bottom. Which is why students write 2 equations for their arrays (when possible.) Here’s the example used in the lesson:

Students should learn that arrays can be read up and down or side to side.
As you can tell by now, this lesson may have seen “easy” to teach, but because it is mathematics, we have to be extra sure that we are paying attention to all the details, and not unknowingly creating misconceptions along the way. Good teaching comes about when we pay attention to these important little things; avoid it, and your students will emerge with even more misunderstandings than when you began.
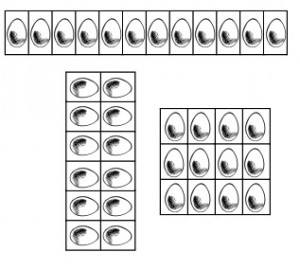
Another matter that is important is making sure students get to practice a new concept in different ways. This could have just printed up another worksheet with cruddy examples (see above), but you know, Robert just don’t roll that way. Instead, there is a “table” where students had scaffolding examples of different ways to solve array problems:
Yes, task cards are fun, but why not have students solve different kinds of array problems, instead of “count and write?”
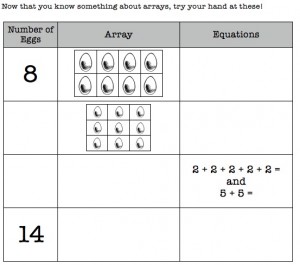
With this all done, thought was given to making sure students should had a chance to do some actual problem solving as part of their lesson on arrays. Unfortunately, a lot of what passes for problem solving doesn’t actual qualify, because it tends to focus on routine problems with just a crappy cutesy graphic thrown in. This is why Robert came up with the idea of an “egg-act array mystery” which would actually challenge a second grader. Here’s an example:

Example of actual problem solving task using arrays.
As you can see, the idea is that some information about the array has been provided (there are 20 eggs, and there are 4 in each row; how many rows are there in the array?) and left something for the student to figure out: how many rows would there be in this array? There is also some space for the student to draw the array, as well as prompted them to write two equations which would show the addition problem that emerged from this array. Yes, this is a little more tricky than the typical “draw and count” task, but isn’t the whole goal of this lesson to challenge students to think on a higher level? By the way, did you notice the equations for the arrays was written “20 eggs = _________” instead of “___________ = 20 eggs?” Yeah, that’s what we mean by expanding a concept.
Finally, students were invited to write their own “array mysteries,” because what good is giving students a task if they can’t come up with one of their own? It is also an excellent way to assess whether the student actually understands the task at hand (and believe me, there are lots of students who are winging their way though math class, which makes this step even more important.)

For assessment, students write and solve their own “array mystery” problems.
So there you have it: a CoCoStaSta lesson that develops concepts, avoids fussy or confusing directions, and provides practice and challenge for everyone. Now, that wasn’t so hard, was it?
 This rant has been brought to you by the guy who published this “Egg-act Arrays” on TeachersPayTeachers for the low, low price of $3.95. When you consider how much actual thought (and not cutesy fonts and graphics) went into this, you’ll understand why you are going to buy it….)
This rant has been brought to you by the guy who published this “Egg-act Arrays” on TeachersPayTeachers for the low, low price of $3.95. When you consider how much actual thought (and not cutesy fonts and graphics) went into this, you’ll understand why you are going to buy it….)
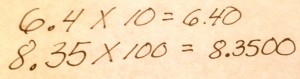



 As Robert tells it, fractions had a good run, and with a 5,000+ year history, they’ve outlived every fad imaginable, including paisley togas and virgin sacrifices. Fractions began their long run with the Egyptians, who utilized them to divide up plots of land and levy taxes. The ancient Sumerians loved fractions so much that they invented the 24 hour day, the 60 minute hour and the 360 degree circle just so they could divide them up into equal pieces really easily: a 24 hour day can be divided into halves, thirds, quarters, sixths, 8ths, 12ths and 24ths (don’t get me started on how easy it is to divide 60 and 360….) You just can’t do that with 10 or 100.
As Robert tells it, fractions had a good run, and with a 5,000+ year history, they’ve outlived every fad imaginable, including paisley togas and virgin sacrifices. Fractions began their long run with the Egyptians, who utilized them to divide up plots of land and levy taxes. The ancient Sumerians loved fractions so much that they invented the 24 hour day, the 60 minute hour and the 360 degree circle just so they could divide them up into equal pieces really easily: a 24 hour day can be divided into halves, thirds, quarters, sixths, 8ths, 12ths and 24ths (don’t get me started on how easy it is to divide 60 and 360….) You just can’t do that with 10 or 100.