Robert has been in the teaching game for a long time. A looooong time. Robert has lived through every math fad that has come along, from the “back to basics” movement right through dozens of different math programs including “Chicago Math,” “TERC,’ “Real Math,” “Mathematics in Context,” and numerous others. Let’s put it this way: when he first started teaching, he regularly called Steve Jobs’ secretary for tips on how to install a video card into the Apple IIe….. If you don’t know what the words “secretary,” “video card” and “Apple IIe” mean, you’ll know that was a long time ago….
Believe it or not, Robert keeps some of his old textbooks he used in his teaching library, and every once in a while he pulls one down for either inspiration or, more likely, to roll his eyes and mutter under his breath, “what was I thinking when I taught this?” Here’s one page that especially embarrasses him from a textbook he used in…. wait for it…. 1985!
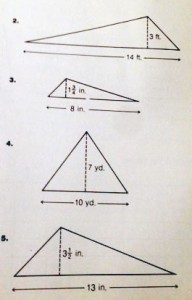
These kinds of problems make Robert go “arrrrghhh!” and not like a silly pirate….
Robert, older and wiser, looks at this exercise and knows that this is junk, junk, junk. “Why are there pictures of triangles?” he mutters under his breath. “Don’t the writers know that the students don’t need the illustrations? They’ll just multiply the two numbers together and divide by two to get the answer.”
This is what irks Robert about how math curriculum is designed: the assumption that students are too stupid to actually think through a few steps of their own to get to a solution. So instead of having them figure out what information is important and how it should be used, they just follow a “rule” over and over and over and over again. Of course, this was back in 1985, so surely things are much better now.
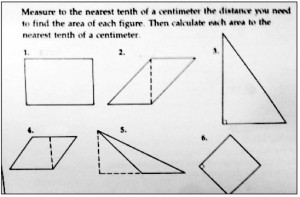
Some improvement, but still not there yet….
Well, maybe a little better. Let’s have a look at this example, which appeared in textbook from 1990. Okay, it’s a bit better: the student actually gets to do something besides “plug and chug” a formula four times in a row, and the student does have to think about whether it should be “basetimesheight” or “basetimesheightdividedbytwo.” The student even gets to make some measurements using a centimeter ruler and round the measurements to the nearest tenth. Hey, look ma, mixed practice AND measurement in one activity!
But do you see why this exercise is a fail? Look closely: what are all those dashed lines doing there? Oh, those are the “height lines,” because we all know that asking students to both measure the parts of a geometric figure and apply a simple formula is really pushing them too hard. Let’s just make it easy on them by showing them what to measure! Damn, Daniel, that’s sad!
Let’s jump ahead 25 years and see how things have changed. Robert enters the terms “practice” and “area of a triangle” into his browser and copies one of the first worksheets to pop up. To protect the guilty, he has eliminated the author’s name (assuming it was an actual person and not a computer program that generated this atrocity.)
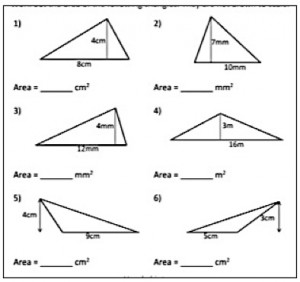
It’s 2016, and our students are still doing junk like this?
25 years later! Think about all the changes that has happened, including 6 presidential elections, several wars, the demise of Wilson Philips and the rise of Ariana Grande, and we’re still giving students the exact same dumbed-down tasks? If anything, this one is even more frivolous, because the measurements don’t include decimals, AND the units for the solutions are written out for the student already. Good grief, thinks Robert, what is the point of it all? Basically, these 6 problems are about as relevant to understanding mathematics as using “Grand Theft Auto” would be in a defensive driving course.
This is what Robert does when you use “dumb” worksheets in your class…..
I fix Robert a cup of chamomile tea, pass him his favorite stress toy and wait.
…and wait…
…and wait…
When he’s sufficiently lucid, I ask Robert to tell me what he does when he designs activities involving area of polygons for his students.
“Well, the first thing is that while the formula for finding the area of shapes like triangles and parallelograms involves base and height, the fact is that any part of these shapes can be the base; the height then has to be drawn in or located. These dumb worksheets do all the work for the student: shouldn’t the students learn for themselves how to identify these parts?”
If you said the base of this triangle was on the bottom, you would be wrong!
That sounds fair: there have been so many times when I’ve looked at problem that my teacher gave me and wondered, “what would happen if I rotated this triangle? Would a different side become the base? And what is the difference between a ‘base’ and a ‘side,’ anyway?”
Robert doesn’t stop there. “What’s going to happen if the student ever has to find the area of a triangle in real life? She’ll be totally lost, because no one told her which side is the base and which part is the height. Then you have kids making very basic mistakes, like believing that the height is just one of the sides, which can be true when the triangle is a right triangle and you use one of the legs (the non-hypotenuse side) as the base. But what if you can’t measure those sides, for some reason? You’re completely stuck, because the problem doesn’t look exactly like the one in the textbook!”
All of which is why Robert is more likely to give the following problem to his students:
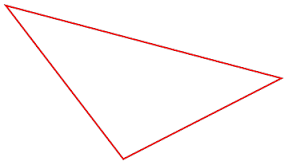
Identify the base and height of this triangle, measure to the nearest tenth of a centimeter, and then calculate the area. Do the problem using three different sets of measurements.
“I’ll admit, this is a tricky problem,” Robert explains, “because it doesn’t spoon feed your students all the information needed to solve it. But isn’t that the point? Shouldn’t we get students beyond the lame ‘plug & chug’ arithmetic and have them really think about mathematics?”
And with that, Robert unwraps a new stress toy and invokes a meme….

Readers who took the time to read and understand this post would most likely like to support the ongoing team of therapist who keep Robert under control by purchasing some of these materials to use in their classroom:
















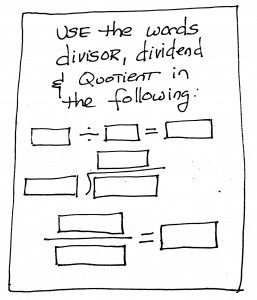

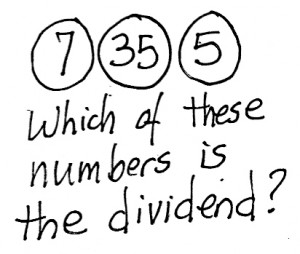









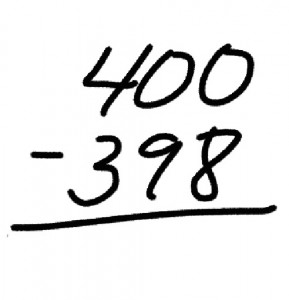

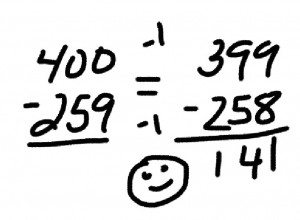






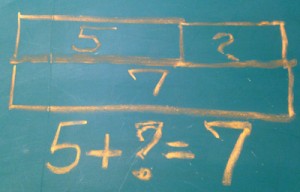
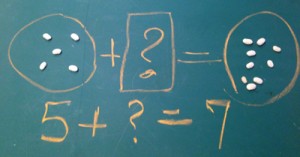 Both models to the right can be used to solve the problem described above. The top one uses a “bar model” which is attributed to the Singapore Math program, but was actually developed by
Both models to the right can be used to solve the problem described above. The top one uses a “bar model” which is attributed to the Singapore Math program, but was actually developed by



